C16.EB1 : Forages de puits
Cet exercice porte sur la notion de listes, la récursivité et la programmation dynamique.
Pour extraire de l’eau dans des zones de terrain instable, on souhaite forer un conduit dans le sol pour réaliser un puits tout en préservant l’intégrité du terrain. Pour représenter cette situation, on va considérer qu’en forant à partir d’une position en surface, on s’enfonce dans le sol en allant à gauche ou à droite à chaque niveau, jusqu’à atteindre le niveau de la nappe phréatique.
Le sol pourra donc être représenté par une pyramide d’entiers où chaque entier est le score de confiance qu’on a dans le forage de la zone correspondante. Une telle pyramide est présentée sur la figure 1, à gauche, les flèches indiquant les différents déplacements possibles d’une zone à une autre au cours du forage.
Un conduit doit partir du sommet de la pyramide et descendre jusqu’au niveau le plus bas, où se situe l’eau, en suivant des déplacements élémentaires, c’est-à-dire en choisissant à chaque niveau de descendre sur la gauche ou sur la droite. Le score de confiance d’un conduit est la somme des nombres rencontrés le long de ce conduit. Le conduit gris représenté à droite sur la figure 1 a pour score de confiance \(4+2+5+1+3=15\).
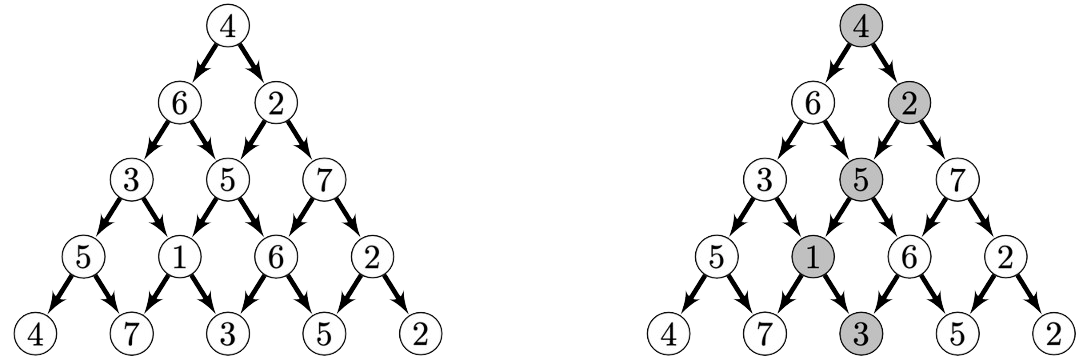
On va utiliser un ordinateur pour chercher à résoudre ce problème. Pour cela, on représente chaque niveau par la liste des nombres de ce niveau et une pyramide par une liste de niveaux.
La pyramide ci-dessus est donc représentée par la liste de listes :
ex1 = [[4],[6,2],[3,5,7],[5,1,6,2],[4,7,3,5,2]]
1. Dessiner la pyramide représentée par la liste de listes : ex2 = [[3],[1,2],[4,5,9],[3,6,2,1]]
2. Déterminer un conduit de score de confiance maximal dans la pyramide ex2 et donner son score.
On souhaite déterminer le score de confiance maximal pouvant être atteint pour une pyramide quelconque. Une première idée consiste à énumérer tous les conduits et à calculer leur score pour déterminer les meilleurs.
3. Énumérer les conduits dans la pyramide de trois niveaux représentée sur la figure 2.
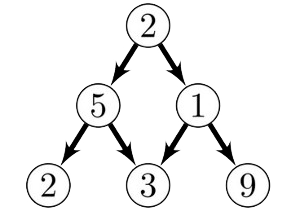
Afin de compter le nombre de conduits pour une pyramide de n niveaux, on remarque qu’un conduit est uniquement représenté par une séquence de n déplacements gauche ou droite.
4. En considérant un codage binaire d’un tel conduit, où gauche est représenté par 0 et droite par 1, déterminer le nombre de conduits dans une pyramide de n niveaux.
5. Justifier que la solution qui consiste à tester tous les conduits possibles pour calculer le score de confiance maximal d’une pyramide n’est pas raisonnable.
On dira dans la suite qu’un conduit est maximal si son score de confiance est maximal. Afin de pouvoir calculer efficacement le score maximal, on peut analyser la structure des conduits maximaux.
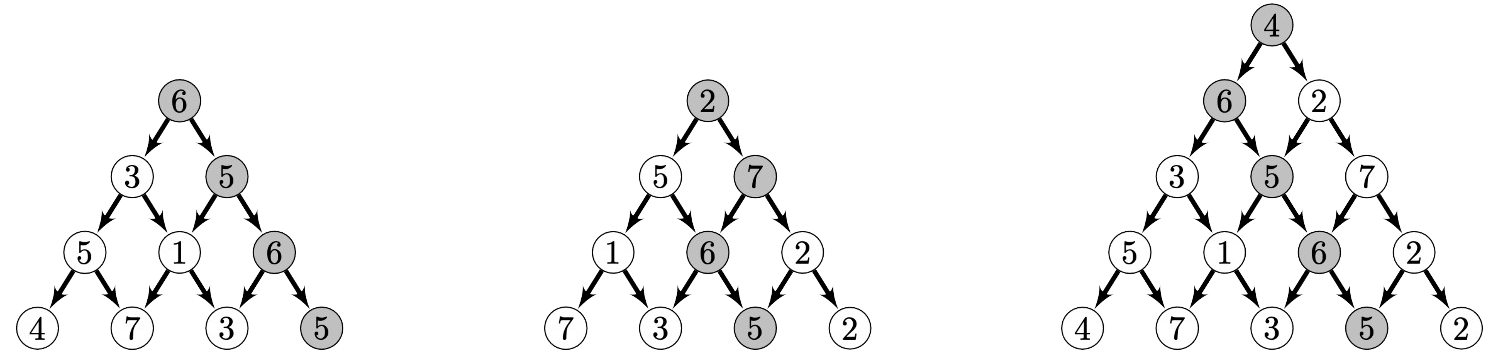
· Première observation : si on a des conduits maximaux cm1 et cm2 (représentés en gris dans la figure 3) pour les deux pyramides obtenues en enlevant le sommet de ex1, on obtient un conduit maximal en ajoutant le sommet 4 devant le conduit de plus grand score parmi cm1 et cm2. Ici le score de cm1 est \(6+5+6+5=22\) et le score de cm2 est \(2+7+6+5=20\) donc le conduit maximal dans ex1 est celui obtenu à partir de cm1 et dessiné à droite dans la figure 3.
· Deuxième observation : si la pyramide n’a qu’un seul niveau, il n’y a que le sommet, dans ce cas, il n’y a pas de choix à faire, le seul conduit possible est celui qui contient le sommet et le nombre de ce sommet est le score maximal que l’on peut obtenir.
Avec ces deux observations, on peut calculer le score maximal possible pour un conduit dans une pyramide p par récurrence. Posons score_max(i,j) le score maximal possible depuis le nombre d’indice j du niveau i, c’est-à-dire dans la petite pyramide issue de ce nombre. On a alors les relations suivantes :
- •
score_max(len(p)-1,j,p) = p[len(p)-1][j]; - •
score_max(i,j,p) = p[i][j] + max(score_max(i+1,j,p),score_max(i+1,j+1,p)).
Le score maximal possible pour p toute entière sera alors score_max(0,0,p).
6. Écrire la fonction récursive score_max qui implémente les règles précédentes.
Si on suit à la lettre la définition de score_max, on obtient une résolution dont le coût est prohibitif à cause de la redondance des calculs. Par exemple score_max(3,1,p) va être calculé pour chaque appel à score_max(2,0,p) et score_max(2,1,p). Pour éviter cette redondance, on décide de mettre en place une approche par programmation dynamique. Pour cela, on va construire une pyramide s dont le nombre à l’indice j du niveau i correspond à score_max(i,j,p), c’est-à-dire au score maximal pour un conduit à partir du nombre correspondant dans p.
7. Écrire une fonction pyramide_nulle qui prend en paramètre un entier n et construit une pyramide remplie de 0 à n niveaux.
8. Compléter la fonction prog_dyn ci-dessous qui prend en paramètre une pyramide p, et qui renvoie le score maximal pour un conduit dans p. Pour cela, on construit une pyramide s remplie de 0 de la même taille et la remplit avec les valeurs de score_max en commençant par le dernier niveau et en appliquant petit à petit les relations données ci-dessus.
def prog_dyn(p):
n = len(p)
s = ...
# remplissage du dernier niveau
for j in ...
s[n-1][j] = ...
# remplissage des autres niveaux
for i in ...
for j in ...
s[i][j] = ...
# renvoie du score maximal
return s[0][0]9. Montrer que le coût d’exécution de cette fonction est quadratique en n pour une pyramide à n niveaux.
10. Expliquer comment adapter la fonction score_max pour éviter la redondance des calculs afin d’obtenir également un coût quadratique, tout en gardant une approche récursive.