C7.3 : Représentation des entiers relatifs
Activité sans ordinateur et sans calculatrice
Prendre connaissance
La représentation d'un nombre entier relatif se fait avec un nombre de bits définit à l'avance.
Exemple avec 4 bits
Avec 4 bits, on dispose de \(2^4 = 16\) valeurs.
On choisit de représenter les entiers relatifs de \(-8\) à \(7\).
| \(nb\) en base 10 | Représentation binaire de \(nb\) | |||||||
|---|---|---|---|---|---|---|---|---|
|
\(nb\) est positif |
7 |
Passage en base 2
←———————— |
0111 | Le bit de poids fort est 0 | ||||
| 6 | 0110 | |||||||
| 5 | 0101 | |||||||
| 4 | 0100 | |||||||
| 3 | 0011 | |||||||
| 2 | 0010 | |||||||
| 1 | 0001 | |||||||
| 0 | 0000 | |||||||
| \(nb\) est négatif | -1 |
Valeur absolue
←—— |
1 |
en base 2
←—— |
0001 |
Cplt à 2
←—— |
1111 | Le bit de poids fort est 1 |
| -2 | 2 | 0010 | 1110 | |||||
| -3 | 3 | 0011 | 1101 | |||||
| -4 | 4 | 0100 | 1100 | |||||
| -5 | 5 | 0101 | 1011 | |||||
| -6 | 6 | 0110 | 1010 | |||||
| -7 | 7 | 0111 | 1001 | |||||
| -8 | 8 | 1000 | 1000 | |||||
Obtenir le complément à 2 d'un nombre binaire
L'obtention du complément à 2 d'un nombre binaire se fait en deux étapes :
- - on inverse tous les bits
- - on ajoute 1
Méthode générale de l'encodage en complément à 2 avec \(n\) bits
• Avec \(n\) bits on dispose de \(2^n\) combinaisons. On choisit de représenter les entiers relatifs de \(-2^{n-1}\) à \(2^{n-1}-1\).
• Passage du nombre entier relatif à la représentation :
Méthode :
- ➩ Si le nombre est positif, alors il faut le convertir en base 2.
- ➩ Si le nombre est négatif, alors il faut prendre sa valeur absolue, puis passer en base 2, puis prendre le complément à 2.
Schéma de la méthode :
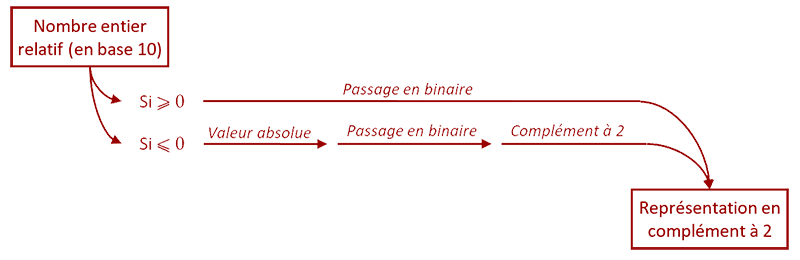
Remarque :
- Le bit de poids fort de la représentation d'un entier positif est toujours 0, alors que celui d'un nombre entier négatif est toujours 1.
• Passage de la représentation au nombrer entier relatif :
Méthode :
- ➩ Si le bit de poids fort de la représentation est 0, alors le nombre est la valeur décimale de la représentation.
- ➩ Si le bit de poids fort de la représentation est 1, alors il faut prendre le complément à 2, puis passer en base 10, puis multiplier par \(-1\).
Schéma de la méthode :

Remarques
La représentation des nombres entiers relatifs présentée ci-dessus et utilisée en informatique permet :
- - de n'avoir qu'une seule représentation pour le nombre 0 ;
- - de conserver l'addition des nombres.
Applications pour bien comprendre
Dans toutes cette partie, on travaillera sur 8 bits.
1) Combien d'entiers relatifs peut-on représenter ? En donner la liste ?
2) Donner les représentations binaires en complément à 2 des nombres 125 et -125.
3) Donner les valeurs décimales des nombres dont les représentations binaires en complément à 2 sont les suivants :
- a/ 1111 1111
- b/ 0000 0000
- c/ 1001 1001
- d/ 0110 0111
4) On s'intéresse au nombre relatif dont la représentation binaire en complément à 2 est 1010 0101
- a/ Ce nombre est-il positif ou négatif ?
- b/ Donner la représentation binaire de l'opposé de ce nombre.
Additionner des entiers relatifs
Dans toutes cette partie, on travaillera sur 6 bits.
1) Combien d'entiers relatifs peut-on représenter ? En donner la liste ?
2) Donner la représentation binaire en complément à 2 des entiers relatifs -18 et -12.
3) A l'aide d'une addition en binaire, trouver la représentation binaire en complément à 2 de la somme de -18 et -12.
4) Cette addition est-elle correcte (détailler la démarche).
Outils
L'outils en ligne suivant permet de connaitre les différentes valeurs possibles correspondant à un représentation machine et inversement : hexed.it