C7.4 : Représentation des nombres à virgule
Python fait-il des calculs corrects ?
Mise en évidence
💻 Evaluer les instruction suivantes :
>>>1.1 + 1.1
>>>1.1 + 1.1 + 1.1Les résultats vous semble-t-ils normaux ?
💻 Evaluer les instruction suivantes :
>>>0.1 + 0.1 - 0.2
>>>0.1 + 0.1 + 0.1 - 0.3Les résultats vous semble-t-ils normaux ?
💻 Evaluer les instruction suivantes :
>>>3 + 10**(-16) == 3
>>>3 + 10**(-15) == 3Les résultats vous semble-t-ils normaux ?
Bilan
...
...
Prendre connaissance
Valeur en base 10 d'un nombre à virgule écrit en base 2
Exemples
Exemple d'un nombre à virgule écrit en base 10 : le nombre \(\pu{83,14}\) peut s'écrire : \(8×10^1+3×10^0+1×\frac{1}{10^1}+4×\frac{1}{10^2}\)
Exemple d'un nombre a virgule écrit en base 2 : le nombre \(\pu{10,011}\) peut s'écrire : \(1×2^1+0×2^0+0×\frac{1}{2^1}+1×\frac{1}{2^2}+1×\frac{1}{2^3}\)
Généralisation
La valeur en base 10 du nombre qui s'écrit \(a_n…a_2\ a_1\ a_0\ ,b_1\ b_2\ b_3…\) en base \(x\) est donné par la relation :
\(a_n…a_2\ a_1\ a_0\ ,b_1\ b_2\ b_3…=a_n×2^n+…+a_2×2^2+a_1×2^1+a_0×2^0+b_1×\frac{1}{2^1}+b_2×\frac{1}{2^2}+b_3×\frac{1}{2^3}+…\)
Cette relation permet de calculer la valeur en base 10 d'un nombre à virgule écrit en base 2.
Valeur en base 2 d'un nombre à virgule écrit en base 10
Généralité
L'écriture un base 2 d'un nombre à virgule écrit en base 10 nécessite :
- - de convertir la partie entière (partie avant la virgule) en base 2 (nous avons déjà vu cela) ;
- - de convertir la partie après la virgule en base 2.
Conversion de la partie après la virgule en base 2
La conversion d'une partie décimale en base 2 se fait par des multiplications successives par 2.
Exemple du nombre 3,14 :

S'entrainer pour bien comprendre
• Donner en base 10 la valeur du nombre à virgule qui s'écrit 111,111 en binaire.
• Donner en base 10 la valeur du nombre à virgule qui s'écrit 1010,1010 en binaire.
• Écrire, en binaire, le nombre dont la valeur en base 10 est 5,25 (on s'arrêtera à 4 bits pour la partie décimale).
• Écrire, en binaire, le nombre dont la valeur en base 10 est 8,8 (on s'arrêtera à 4 bits pour la partie décimale).
Remarque
Un nombre qui a un nombre de chiffre après la virgule fini lorsqu'on l'écrit en base 10, peut avoir un nombre de chiffre après la virgule infini lorsqu'on souhaite l'écrire en base 2.
Le nombre de bits utilisé pour le codage d'un nombre à virgule étant limité, il y a nécessairement des arrondis. C'est cela qui explique les problèmes de calculs qui ont été soulevés dans la paragraphe I.
Pour aller plus loin : représentation des nombres à virgule
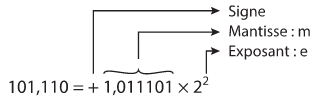
Ecriture normalisée d'un nombre binaire à virgule
L'écriture normalisée d'un nombre à virgule fait apparaître 3 parties :
- - le signe \(s\) (on choisit s = 0 si le nombre est positif et s = 1 si le nombre est négatif) ;
- - la mantisse \(m\) : elle comporte toujours l'unique chiffre 1 avant la virgule ;
- - l'exposant \(e\) (il correspond au décalage de la virgule entre l'écriture du nombre et l'écriture de la mantisse).
Ainsi, tous les nombres à virgule en base 2 peuvent s'écrire sous la forme : \(Nombre = {(-1)}^s × 2^e × m\)
Exemple avec le nombre 101,110 :
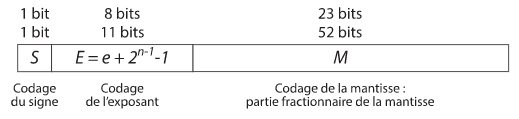
Représentation du nombre sur 32 bits (respectivement 64 bits)
Répartition des bits
Comme pour les entiers relatifs, le nombre de bits utilisé pour la représentation est définit à l'avance.
• 1 bit est réservé pour le code S correspondant au signe.
• 8 bits (respectivement 11 bits) sont réservés pour le code E correspondant à l'exposant.
• 23 bits (respectivement 52 bits) sont réservés pour le code M correspondant à la mantisse.
Codage du signe
Le code S du signe est égale au signe s, autrement dit S = 0 si le nombre est positif et S = 1 si le nombre est négatif.
Codage de l'exposant
Le code E de l'exposant est \(E = e + 2^{n-1} - 1\) (où n est le nombre de bits utilisé pour coder l'exposant). L'ajoute de \(2^{n-1} - 1\) a pour but que E soit toujours un nombre positif, que l'exposant soit positif ou négatif.
Codage de la mantisse
Le code M de la mantisse est celui de la partie après la virgule de la mantisse. Le 1 avant la virgule est omis car il est est présent dans toutes les écritures normalisée des nombres à virgules en binaire.
Bilan
\(Nombre = {(-1)}^s × 2^{E-2^{n-1}+1} × 1,M\)
Applications pour bien comprendre
• Donner la valeur décimale du nombre binaire flottant suivant codé sur 32 bits :
1100 0011 0101 0110 1100 0000 0000 0000
• Donner la valeur décimale du nombre binaire flottant suivant codé sur 64 bits :
0001 0000 0011 1101 0011 1001 0101 1000 0000 0000 0000 0000 0000 0000 0000 0000
Outils
L'outils en ligne suivant permet de connaitre les différentes valeurs possibles correspondant à un représentation machine et inversement : hexed.it