C14.2 : TD - Comment un processeur additionne-t-il deux nombres ?

Quelques repères historiques

1937 : Premier circuit binaire avec deux relais (dispositifs de commutation électromécaniques) proposé par George Stibitz.

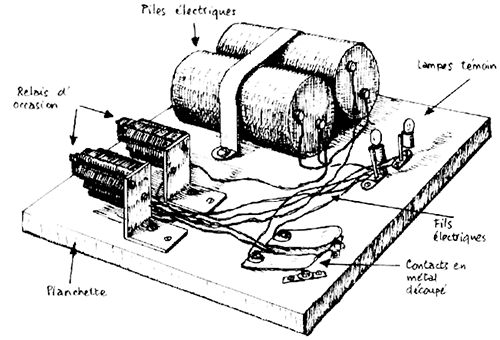
1941 : Mise au point du Z3, première machine programmable utilisant des relais.

Les relais seront ensuite remplacés par des tubes (dispositifs d'amplification et de commutation entièrement électriques) qui, bien que plus fiables que les relais, chauffent énormément.

1942 : Test réussi de l'Atanasoff-Berry Computer (considéré, avec l'ENIAC, comme le premier ordinateur entièrement électronique).

1945 : Finalisation de l'ENIAC (considéré comme le premier ordinateur).

Ces machines ont été les premières à implanter trois concepts fondamentaux :

- utilisation du binaire pour représenter tous les nombres et les données ;

- calculs réalisés par l'électronique plutôt que des éléments mécaniques ;

- une organisation séparée entre la mémoire et l'unité de calcul.

1947 : Invention du transistor (dispositif entièrement électrique) par John Bardeen, William Shockley et Walter Brattain. Plus petit, plus fiable et dégageant moins de chaleur que les relais, les transistors sont encore aujourd'hui les éléments de base des microprocesseurs.

Simulateur

Dans cette activité, une application qui simule les portes logiques est nécessaire.

Lien de téléchargement d'un logiciel de simulation : https://sourceforge.net/projects/circuit/

Le logiciel est portable, c'est à dire qu'il n'a pas besoin d'être installé, il s'execute directement.

Remarque : pour disposer des schémas européens, choisir "File -> Preferences... -> International -> Gate shape: Rectangular"

Autres simulateurs en ligne

D'autres simulateurs existent, en particulier en ligne :

• - simulator.io.
• - logic.ly.

Les opérateurs booléens de base

Rappels

✍ Rappeler la table de vérité de l'opérateur not (opérateur à une entrée).

✍ Rappeler les tables de vérité des opérateurs and, or et xor (opérateurs à deux entrées).

Câblage avec le logiciel de simulation

💻 Câbler chacune des portes logiques et vérifier les tables.

Additionneur 1 bit (ou semi additionneur)

Position du problème

Dans cette partie, on souhaite additionner deux bits, que l'on notera A et B, en vue d'obtenir la somme S et la retenue R de l'opération.

Expressions booléennes

✍ Construire la table correspondant à la somme S de deux bits A et B.

✍ Construire la table correspondant à la retenue R de la somme de deux bits A et B.

✍ Construire les tables des expressions booléennes suivantes :

• • A and B
• • (A and B) or (A and B)
• • A xor B

✍ En déduire les expressions booléennes de S et de R en fonction de A et B.

Lien avec le repère historique

Le premier circuit binaire proposé par G. Stibitz était un additionneur 1 bit.

1) Où sont les entrée correspondant aux deux nombres A et B sur le schéma de G. Stibitz ?

2) Pourquoi y a-t-il deux lampes sur le schéma de G. Stibitz ?

Câblage avec le logiciel de simulation

💻 Câbler les circuits permettant d'obtenir R et S en fonction de A et B.

Remarque : On gardera ce câblage pour la suite, à savoir le VI.

Additionneur 1 bit complet

Position du problème

On souhaite maintenant faire l'addition de deux nombres de 4 bits.

✍ Exemple : faire l'addition de 0001 avec 1011 en posant l'opération et en mettant en évidence les retenues.

✍ Est-il possible de construire un additionneur 4 bits en utilisant 4 additionneur 1 bit ?

Additionneur 1 bit complet

L'additionneur 1 bit complet permet, à partir de deux bits A et B et d'une retenue R_in, d'obtenir la somme S et la retenue R_out.

L'additionneur 1 bit complet sera schématisé ainsi :

✍ Construire la table correspondant à la somme S de trois nombre de 1 bit A, B et R_in.

✍ Construire la table correspondant à la retenue R_out de la somme de trois nombre de 1 bit A, B et R_in.

✍ Justifier que Sn = A xor B xor Rin

✍ Justifier que Rout = (A and B) or (A and Rin) or (B and Rin)

Câblage avec le logiciel de simulation

💻 Câbler les circuits permettant d'obtenir la somme et la retenue R à partir trois bits A, B et R_in.

Remarque : On gardera ce câblage pour la suite, à savoir le VI.

Additionneur 4 bits

Dans la suite, un nombre binaire X sera noté x3x2x1x0 où x0, x1, x2 et x3 sont les 4 bits du nombre.

Schéma

✍ Sur le modèle du schéma du V.2, faire le schéma de l'additionneur 4 bits de deux nombres A (noté a3a2a1a0) et B (noté b3b2b1b0) de 4 bits chacun.

Câblage avec le logiciel de simulation

💻 Câbler les circuits permettant d'obtenir la somme S de deux nombres A et B de 4 bits chacun.

💻 Vérifier l'exemple précédent.