C4.2 : TP Dessins de fractales
Les fractales
Une fractale est un objet dont la structure est invariante par changement d'échelle.
Le mot fractale fait référence à une théorie mathématique précise développée par le mathématicien Benoît Mandelbrot dans les années 1970.
Des formes fractales approximatives se retrouvent dans de nombreux domaines naturels :
- - relief d'une côte maritime
- - plume d'oiseau
- - ...
But du TP : Le but de ce TP est de dessiner quelques fractales à l'aide du module PIL.
Fractales de von Koch
Présentation


Programmation
► La méthode line de PIL
Pour dessiner, on utilisera le module PIL.
Les traits seront tracés à l'aide de la méthode line.
Exemple :
from PIL import Image, ImageDraw
L = 600
H = 300
image = Image.new('RGB', (L, H), (240, 240, 240))
image_dessin = ImageDraw.Draw(image)
image_dessin.line([10,10,L-10,H-10], fill=(255,0,0), width=3)
image.show()► Des dessins en mode Tortue
On va dessiner la courbe de von Koch en programmant une tortue virtuelle qui se déplace en laissant une trace sur son passage.
La tortue virtuelle se caractérise par :
- - une position définie par les grandeurs x et y en pixels ;
- - une orientation définie par un angle α en degrés.
Les actions possibles de la tortue virtuelle sont :
- - se déplacer d'une distance d en pixels en traçant un trait ;
- - changer d'orientation en tourner sur place d'un angle α.
La tortue sera implémentée par une classe Tortue dont les attributs et les méthodes sont données par la structure ci-dessous.
class Tortue:
def __init__(self, dessin, x:float, y:float, a:float):
self.dessin = dessin # objet ImageDraw associé à un objet Image de PIL
self.x = x # abscisse de la Tortue
self.y = y # ordonnée de la Tortue
self.a = a # orientation de la Tortue en degrés (0 = horizontal ; + = sens horaire)
self.couleur = (0,0,0)
self.epaisseur = 2
def trace(self, d:float):
'''
Déplace la Tortue (en partant de sa position et avec son orientation) d'une distance égale à d pixels tout en traçant un trait.
Remarque : cette méthode modifie les attributs x et y de la Tortue.
'''
pass
def tourne(self, ang:float):
'''
Change l'orientation de la Tortue d'un angle a en degrés.
Remarque : cette méthode modifie l'attribut a de la Tortue.
'''
passA faire
1) Compléter le code de la classe ci-dessus. Un peu de trigonométrie sera nécessaire !
2) Pour vous entrainer, écrire le code qui permet de dessiner un carré au centre d'une image à l'aide d'une occurrence de la classe Tortue.
► Utilisation de la récursivité
Les dessins des deux fractales de von Koch se programment facilement en utilisant une fonction récursive.





A faire
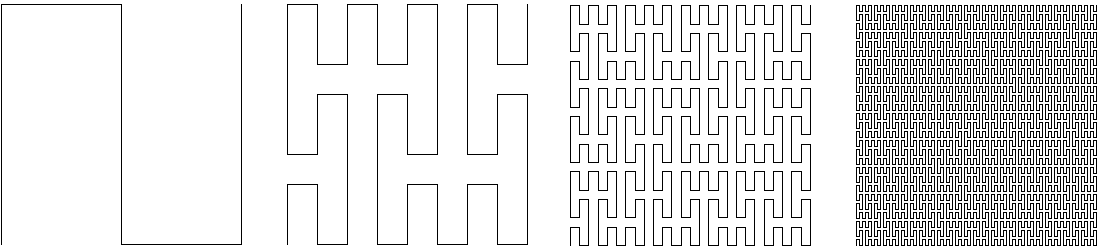
1) Écrire le programme avec une fonction récursive qui permet de dessiner, en mode tortue, la courbe de von Koch à une profondeur donnée.
2) Écrire le programme avec une fonction récursive qui permet de dessiner, en mode tortue, le flocon de von Koch à une profondeur donnée.
Tapis de Sierpinski
Présentation

Programmation
Écrire un fonction récursive qui dessine la fractale ci-dessus.
On pourra utiliser la méthode rectangle de PIL
Exemple :
from PIL import Image, ImageDraw
L = 400
H = 250
image = Image.new('RGB', (L, H), (240, 240, 240))
image_dessin = ImageDraw.Draw(image)
image_dessin.rectangle([50,50,L-50,H-50], fill=(200,0,0), outline=(0,100,200), width=5)
image.show()Quelques exemples supplémentaires