C14.2 : KNN - Principe général

Présentation du problème

Pouvez-vous dire quelle couleur il faut attribuer au point blanc ?

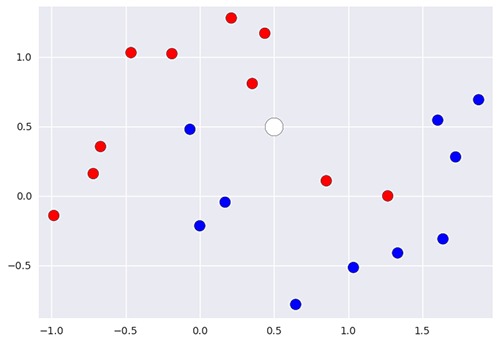
Les algorithmes des k plus proches voisins (k nearest neighbors)

Une façon de résoudre le problème posé consiste à :

• - choisir un nombre entier k,
• - dans la liste des points connus, choisir les k plus proches voisins du point inconnu,
• - compter le nombre de points rouge et de points bleu parmi ces voisins,
• - attribuer la couleur en fonction du plus grand résultat trouvé.

Vocabulaire

Travail à faire

On dispose des données suivantes :

donnees = [{"couleur":"rouge", "position":(-1,-0.1)},
           {"couleur":"rouge", "position":(-0.7,0.2)},
           {"couleur":"rouge", "position":(-0.6,0.3)},
           {"couleur":"rouge", "position":(-0.5,1)},
           {"couleur":"rouge", "position":(-0.2,1)},
           {"couleur":"rouge", "position":(0.2,1.4)},
           {"couleur":"rouge", "position":(0.3,0.8)},
           {"couleur":"rouge", "position":(0.4,1.2)},
           {"couleur":"rouge", "position":(0.8,0.1)},
           {"couleur":"rouge", "position":(1.3,0)},
           {"couleur":"bleu", "position":(-0.1,0.5)},
           {"couleur":"bleu", "position":(0,0.3)},
           {"couleur":"bleu", "position":(0.1,0)},
           {"couleur":"bleu", "position":(0.6,-0.5)},
           {"couleur":"bleu", "position":(1,-0.5)},
           {"couleur":"bleu", "position":(1.3,-0.4)},
           {"couleur":"bleu", "position":(1.6,-0.3)},
           {"couleur":"bleu", "position":(1.6,0.5)},
           {"couleur":"bleu", "position":(1.7,0.3)},
           {"couleur":"bleu", "position":(1.9,0.7)}]

Proposer un programme qui permet de déterminer la couleur d'un point quelconque en se basant sur la méthode des KNN.

Le programme sera découpé en plusieurs fonctions, en particulier pour le calcul de la distance entre deux points.

L'utilisateur devra pouvoir choisir les coordonnées du point ainsi que le nombre K de voisins à considérer.

On complétera le programme avec une fonction qui permet de visualiser les données en utilisant le module Mathplotlib.

Prolongement : les calculs de distance

Généralités

Le choix du nombre de voisin à considérer est l'un des paramètres important de l'algorithme.

Il y en a un autre : le choix de l'algorithme pour calculer la distance entre deux points.

Exemples de calculs pour les distances

Considérons un point \(x\) caractérisé par n valeurs \(x_i\) et un point \(y\) par n valeurs \(y_i\).

Distance euclidienne : \(d_{eucl} = \sqrt{\sum\limits_{i=1}^{n} (y_i-x_i)^2}\)

Distance de Manhattan : \(d_{manh} = \sqrt{\sum\limits_{i=1}^{n} \lvert y_i-x_i \rvert}\)

Travail à faire

Compléter votre programme précédent avec une fonction qui calcul la distance de Manhattan entre deux points.