C10.2 : Calculabilité et décidabilité
Problématique du chapitre
Est-ce que tous les problèmes mathématiques peuvent être résolus par des algorithmes ?
Fonction calculable
Une fonction est calculable si le calcul des images peut être fait pour tous les arguments de façon précise et en un nombre fini d'étapes.
Remarque :
Il reste à définir la méthode de calcul.
Plusieurs propositions ont été faites, on citera :
- - le λ-calcul (1930, par Alonzo Church) ;
- - la machine de Turing (1936, Alan Turing)...
Alonzo Church a postulé (années 1930) que ces deux méthodes, avec quelques autres, sont équivalentes.
On admettra que les langages de programmation actuels (JavaScript, C, Perl, Java, Fortran, etc) sont aussi des méthodes de calculs valables.
Ainsi, de façon simplifiée, on va dire qu'une fonction est calculable si le calcul des images peut être fait pour tous les arguments dans l'un ou l'autre des langages usuels.
Décidabilité
Les problèmes de décision
Un problème de décision est une question mathématique dont la réponse est "oui" ou "non".
Les objets sur lesquels portent le problème sont appelés les instances du problème et doivent être définis précisément.
Les problèmes de décision décidables
On dit qu'un problème de décision est décidable s'il existe un algorithme qui se termine en un nombre fini d'étapes pour chaque instance du problème.
Remarque : Cette définition revient à dire que la fonction qui correspond au problème de décision est calculable.
Exemples
Primalité d'un nombre
➤ Étant donné un nombre entier naturel, ce nombre est-il premier ?
Remarque : les instances de ce problème de décision sont les nombres entiers naturels.
Ce problème de décision est-il décidable ?
🖳 Proposer un programme python pour le démontrer.
Graphe hamiltonien
➤ Étant donné un graphe non orienté, est-il possible de trouver un cycle passant une seule fois par chaque sommet ?
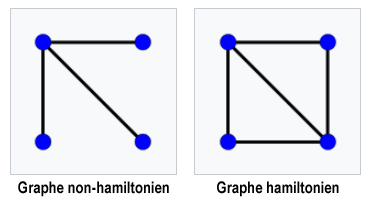
Remarque : les instances de ce problème de décision sont des graphes.
Ce problème de décision est-il décidable ? Oui, mais nous ne le montrerons pas ici.
Les programmes comme données
Présentation
Un programme (écrit en Python par exemple) n’est autre qu’une chaîne de caractères : c’est le texte même du programme.
Or les chaines de caractères peuvent être utilisées en paramètre des fonctions d'un programme.
Finalement, les programmes peuvent utiliser d'autres programmes comme données.
A faire :
Citer d'autres exemples de programmes qui prennent des programmes comme données.
Exemple en python
Exemple d'utilisation de code présent dans une chaine de caractères :
program = '''
for i in range(3):
print("Le Python, c'est cool :-)")
'''
exec(program)
Exemple de passage d'une fonction en paramètre d'une autre fonction :
from math import sqrt
def f1(x:float)->float:
return x ** 2
def f2(x:float)->float:
return sqrt(x)
def f3(x:float)->float:
return x + 2
def g(f, a:float)->float:
return x * f(a)
# Programme principal
print('f1(2) = ' + str(g(f1, 2)))
print('f2(2) = ' + str(g(f2, 2)))
print('f3(2) = ' + str(g(f3, 2)))Le problème de l'arrêt
Tous les problèmes de décisions sont-ils décidables ?
Présentation du problème
Compte tenu du fait que les programmes qui ne se terminent pas peuvent avoir des conséquences fâcheuses, est-il possible de concevoir un programme disant si l'execution d'un autre programme se termine ou non ?
Ce problème, que l'on appelle "Problème de l'arrêt" est un problème de décision pour lequel les instances sont les programmes.
Démonstration de l'indécidabilité du problème de l'arrêt
Nous allons faire une démonstration par l'absurde.
• Supposons que l'on ait codé la fonction testArret(prog, x) suivante qui permet de tester si la fonction fct appliquée à x s'arrête, c'est-à-dire fct(x) s'arrête.
Remarque : x doit être du même type que le paramètre de la fonction fct
def testARRET(fct, x):
...
# si fct(x) s'arrête : resultat = True
# si fct(x) ne s'arrête pas : resultat = False
return resultat• Considérons maintenant la fonction testSurSoi(fct) qui prend une fonction en paramètre et dont le code est donné ci-dessous.
def testSurSoi(f):
if testArret(f, f):
while True:
pass
else:
return True• Lançons maintenant l'instruction ci-dessous.
testSurSoi(testSurSoi)➤ Raisonnement
• Supposons que l'instruction testSurSoi(testSurSoi) se termine.
Alors le test de la ligne 2 va renvoyer True.
Dans ce cas, les lignes 3 et 4 vont s'exécuter, or elles font une boucle qui ne s'arrête jamais.
On peut donc affirmer que l'instructiontestSurSoi(testSurSoi) que l'on vient d'exécuter ne se termine jamais, ce qui est en contradiction avec notre hypothèse.
• Supposons que l'instruction testSurSoi(testSurSoi) ne se termine pas.
Alors le test de la ligne 2 doit renvoyer False.
Dans ce cas, la ligne 6 va s'exécuter.
On peut donc affirmer que l'instructiontestSurSoi(testSurSoi) que l'on vient d'exécuter se termine, ce qui est en contradiction avec notre hypothèse.
• Bilan : le seul point hypothétique de notre raisonnement est l'existence de la fonction testArret(). On peut donc affirmer que cette fonction ne peut pas exister : le "Problème de l'arrêt" est donc indécidable.
➤ Autre raisonnement