C7.4 : Complexité - Généralités

Rappels : qu'est-ce que la complexité (le coût) d'un algorithme ?

■ Valider un algorithme

Lorsqu'on écrit un algorithme, trois questions fondamentales se posent :

- Est-ce qu'il se termine => C'est ce que l'on appelle la terminaison.
- Est-ce qu'il donne le résultat attendu => C'est ce que l'on appelle la correction.
- Est-ce qu'il donne le résultat en utilisant des ressources (principalement du processeur et de la mémoire...) raisonnables => C'est ce que l'on appelle la complexité.

Nous allons reprendre plus en détail la notion de complexité d'un algorithme (que l'on appelle aussi le coût) du point de vue des ressources processeur.

■ Définition

Le coût (du point de vue des ressources du processeur) d'un algorithme est le nombre d'opérations élémentaires effectuées par un algorithme.

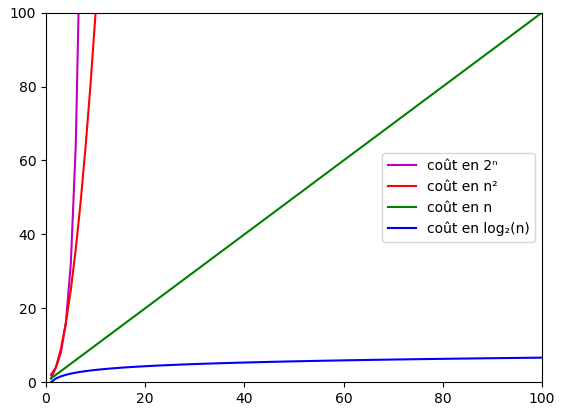
■ Évolution du coût en fonction de la taille des données traitées

Connaite le coût d'un algorithme est particulièrement important lorsque les algorithmes traitent des données de taille variable. Dans ce cas, il est important de savoir comment le coût varie en fonction la taille des données.

Les principales évolutions que l'on rencontre sont, en notant \(n\) la taille des données :

- coût constant,
- coût logarithmique : le coût est proportionnel à \(\log_2 n\),
- coût linéaire : le coût est proportionnel à \(n\),
- coût quadratique : le coût est proportionnel à \(n^2\),
- coût exponentiel : le coût est proportionnel à \(2^n\)

■ Pire cas et meilleur cas

La taille des données traitées n'est pas le seul paramètre dont peut dépendre le coût d'un algorithme.

Par exemple, pour une liste, l'ordre des valeurs peut modifier le coût. Trier dans l'ordre croisant la liste [1, 2, 3, 4] ou la liste [3, 4, 1, 2] peut ne pas avoir le même coût suivant l'algorithme utilisé.

Ainsi, pour un algorithme donné, on distingue le pire cas (celui dont le coût est le plus élevé) et le meilleur cas (celui dont le coût est le plus faible).

Applications

Application 1 : somme des valeurs d'une liste

On s'intéresse à l'algorithme classique qui permet d'obtenir la somme des valeurs d'une liste d'entiers.

1) Écrire une fonction qui prend une liste d'entiers en paramètre et renvoie la somme des valeurs de cette liste.

2) Quel est le coût votre l'algorithme en fonction de la longueur de la liste.

Application 2 : recherche du max

On s'intéresse à l'algorithme classique de recherche de la valeur maximale d'une liste d'entiers.

1) Écrire une fonction qui prend une liste d'entiers en paramètre et renvoie la plus grande valeur de cette liste en fonction de la longueur de la liste.

2) Quel est, dans le pire cas, le coût votre l'algorithme.

3) Quel est, dans le meilleurs cas, le coût votre l'algorithme en fonction de la longueur de la liste.

Application 3 : somme des valeurs d'une liste de listes

On souhaite travailler avec des matrices d'entiers de taille \(n×n\) que l'on implémente par des listes de listes d'entiers.

1) Écrire une fonction somme_matrice(m) qui prend une matrice contenant des entiers en paramètre et renvoie la somme des valeurs de cette matrice.

Exemple

>>> m1 = [[1, 2], [5,6]]
>>> somme_matrice(m1)
14

2) Quel est le coût votre l'algorithme en fonction de la taille n de la matrice passée en paramètre.

Application 4 : fonction mystère

On s'intéresse à la fonction dont le code est donné ci-dessous.

def dec_to_bin(nb):
    chaine = ""
    while nb > 0:
        r = nb % 2
        nb = nb // 2
        chaine = str(r) + chaine
    return chaine

1) Analyser la fonction et écrire sa docstring.

2) Combien de fois la boucle de cet algorithme est-elle exécutée en fonction du paramètre nb ?