C5.3 : Arbres binaires de recherche ABR

Définition d'un Arbre Binaire de Recherche (ABR)

Un arbre binaire de recherche (ABR) est un arbre binaire tel que :

- les valeurs du sous-arbre de gauche sont inférieures ou égales à la valeur de la racine ;
- les valeurs du sous-arbre de droite sont strictement supérieures à la valeur de la racine ;
- les sous-arbres de gauche et de droite sont eux-mêmes des arbres binaires de recherche.

Q1 : L'arbre ci-dessous est-il un arbre binaire ? Est-il un arbre binaire de recherche ?

Afficher la correction

Oui, c'est un arbre binaire de recherche.

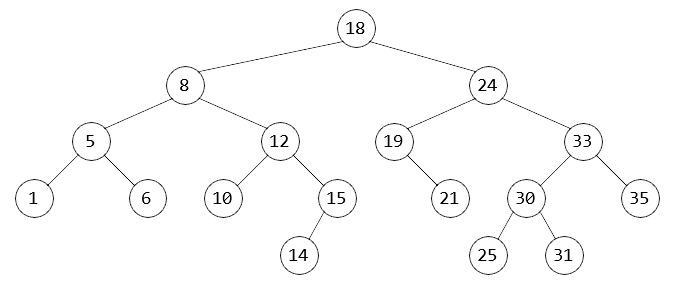
Q2 : Construire deux ABR différents avec tous les entiers de 1 à 10.

Q3 : Afficher les valeurs dans l'ordre du parcours infixe. Qu'observez-vous ?

Afficher la correction

Avec le parcours infixe, les valeurs sont affichées dans l'ordre croissant.

Recherche d'une valeur dans un ABR

Dans cette partie, on souhaite pouvoir rechercher une valeur dans un ABR.

On travaillera avec une implémentation des arbres binaires à l'aide de tuples imbriqués, avec None pour l'arbre est vide.

Algorithme de la recherche d'une valeur dans un ABR

Q4 : Écrire une fonction récursive qui permet de savoir si une valeur est dans un ABR. La fonction prendra deux paramètres : un tuple correspondant à un arbre, la valeur recherchée.

Afficher la correction

def est_dans(arbre, val):
    if arbre == None:
        return False
    elif arbre[0] == val:
        return True
    elif val < arbre[0]:
        return est_dans(arbre[1], val)
    else:
        return est_dans(arbre[2], val)

# ===== Programme principal ====
arbre = (18,(8,(5,(1,None,None),(6,None,None)),(12,(10,None,None),None)),(24,(19,None,(21,None,None)),(33,(30,None,None),(35,None,None))))

print(est_dans(arbre, 0) == False)
print(est_dans(arbre, 1) == True)
print(est_dans(arbre, 3) == False)
print(est_dans(arbre, 8) == True)
print(est_dans(arbre, 13) == False)
print(est_dans(arbre, 17) == False)
print(est_dans(arbre, 20) == False)
print(est_dans(arbre, 21) == True)

Q5 : Appliquer la fonction à l'arbre ci-dessous en recherchant les valeurs 8, 13 et 17 :

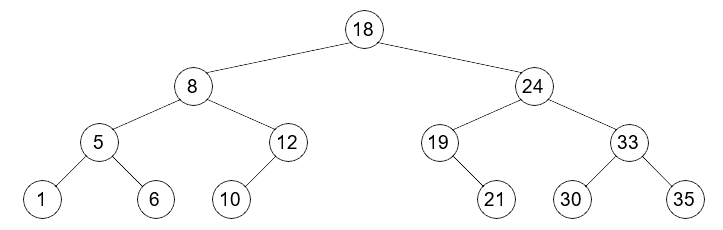
Q6 : Combien de fois se fait l'appel récursif dans le pire cas en fonction de la hauteur de l'arbre ?

Afficher la correction

Dans le pire cas, l'appel de la fonction récursive se fait un nombre de fois égal à la hauteur de l'arbre plus 1.

ABR équilibré

Q7 : On considère les deux ABR ci-dessous dont les valeurs sont identiques. Dans lequel la recherche sera-t-elle globalement la plus efficace ?

Afficher la correction

La recherche sera plus efficace pour l'arbre de gauche dont la hauteur est plus petite.

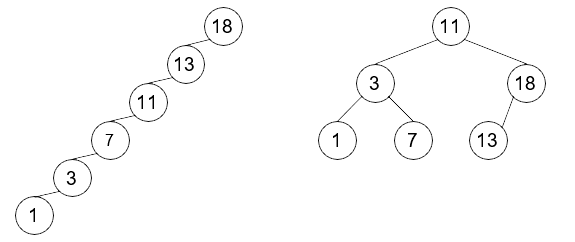
Définition

Un arbre binaire est dit équilibré si :

- les hauteurs du sous-arbre de gauche et du sous-arbre de droite diffèrent au maximum de 1 ;
- les sous-arbres de gauche et de droite sont eux-mêmes équilibrés.

Q8 : Donner un exemple d'ABR équilibré et un exemple d'ABR non équilibré.

Q9 : L'arbre binaire ci-dessous est-il un ABR ? Est-il équilibré ?

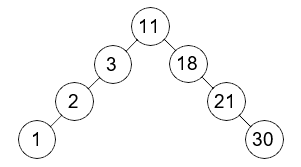
Q10 : Quel peut-être l'intérêt d'un ABR équilibré pour faire une recherche de valeur ?

Ajout d'une valeur dans un ABR

Dans cette partie, on travaillera avec une implémentation des arbres binaires à l'aide de tuples imbriqués, avec None si l'arbre est vide.

Q11 (sur papier) : Ajouter les valeurs 7, 11 et 13 à l'arbre de la question Q5 de façon à conserver son caractère d'ABR.

Q12 : Écrire une fonction qui prend un ABR et une valeur en paramètre et renvoie un ABR correspondant à l'ABR passé en paramètre auquel la valeur a été ajoutée. Si la valeur est déjà dans l'arbre, la fonction doit renvoyer l'ABR sans modification.

Afficher la correction

Version 1 :

import matplotlib.pyplot as plt

def hauteur(t):
    if t == None:
        return 0
    else:
        _, t1, t2 = t
        return max([hauteur(t1), hauteur(t2)]) + 1

def draw_tree_aux(t, rect, dy, labels):
    if t == None:
        return None
    x1, x2, y1, y2 = rect
    xm = (x1 + x2) // 2
    x, t1, t2 = t
    draw_tree_aux(t1, (x1, xm, y1, y2 - dy), dy, labels)
    draw_tree_aux(t2, (xm, x2, y1, y2 - dy), dy, labels)
    if t1 != None:
        a, b = ((xm, (x1 + xm) // 2), (y2, y2 - dy))
        plt.plot(a, b, 'k', marker='o', markersize=20, markerfacecolor='white')
    if t2 != None:
        c, d = ((xm, (x2 + xm) // 2), (y2, y2 - dy))
        plt.plot(c, d, 'k', marker='o', markersize=20, markerfacecolor='white')
    if labels:
        plt.text(xm, y2, str(x), fontsize=10,
                 horizontalalignment='center', verticalalignment='center')

def draw_tree(t, labels=True):
    d = 512
    pad = 20
    dy = (d - 2 * pad) / (hauteur(t))
    draw_tree_aux(t, (pad, d - pad, pad, d - pad), dy, labels)
    plt.axis([0, d, 0, d])
    plt.axis('off')
    plt.show()

def ajoute_v1(arbre, val):
    if val == arbre[0]:
        return arbre
    elif val < arbre[0] and arbre[1] == None:
        return (arbre[0], (val, None, None), arbre[2])
    elif val > arbre[0] and arbre[2] == None:
        return (arbre[0], arbre[1], (val, None, None))
    else:
        if val < arbre[0]:
            return (arbre[0], ajoute_v1(arbre[1], val), arbre[2])
        else:
            return (arbre[0], arbre[1], ajoute_v1(arbre[2], val))

def ajoute_v2(arbre, val):
    if arbre == None:
        return (val, None, None)
    elif val < arbre[0]:
        return (arbre[0], ajoute_v2(arbre[1], val), arbre[2])

    elif val > arbre[0]:
        return (arbre[0], arbre[1], ajoute_v2(arbre[2], val))
    else:
        return arbre


# ===== Programme principal ====
arbre = (18,(8,(5,(1,None,None),(6,None,None)),(12,(10,None,None),None)),(24,(19,None,(21,None,None)),(33,(30,None,None),(35,None,None))))

arbre = ajoute_v2(arbre, -5)
draw_tree(arbre)

Version 2 :

import matplotlib.pyplot as plt

def hauteur(t):
    if t == None:
        return 0
    else:
        _, t1, t2 = t
        return max([hauteur(t1), hauteur(t2)]) + 1

def draw_tree_aux(t, rect, dy, labels):
    if t == None:
        return None
    x1, x2, y1, y2 = rect
    xm = (x1 + x2) // 2
    x, t1, t2 = t
    draw_tree_aux(t1, (x1, xm, y1, y2 - dy), dy, labels)
    draw_tree_aux(t2, (xm, x2, y1, y2 - dy), dy, labels)
    if t1 != None:
        a, b = ((xm, (x1 + xm) // 2), (y2, y2 - dy))
        plt.plot(a, b, 'k', marker='o', markersize=20, markerfacecolor='white')
    if t2 != None:
        c, d = ((xm, (x2 + xm) // 2), (y2, y2 - dy))
        plt.plot(c, d, 'k', marker='o', markersize=20, markerfacecolor='white')
    if labels:
        plt.text(xm, y2, str(x), fontsize=10,
                 horizontalalignment='center', verticalalignment='center')

def draw_tree(t, labels=True):
    d = 512
    pad = 20
    dy = (d - 2 * pad) / (hauteur(t))
    draw_tree_aux(t, (pad, d - pad, pad, d - pad), dy, labels)
    plt.axis([0, d, 0, d])
    plt.axis('off')
    plt.show()

def ajoute(arbre, val):
    if arbre == None:
        return (val, None, None)
    elif val < arbre[0]:
        return (arbre[0], ajoute(arbre[1], val), arbre[2])
    elif val > arbre[0]:
        return (arbre[0], arbre[1], ajoute(arbre[2], val))
    else:
        return arbre

# ===== Programme principal ====
arbre = (18,(8,(5,(1,None,None),(6,None,None)),(12,(10,None,None),None)),(24,(19,None,(21,None,None)),(33,(30,None,None),(35,None,None))))

arbre = ajoute(arbre, 3)
draw_tree(arbre)