C5.5 : TD - Codage de Huffman

On se propose d'étudier une méthode de compression de données inventée par David Albert Huffman en 1952. Cette méthode permet de réduire la longueur du codage d'un alphabet, elle repose sur la création d'un arbre binaire.

On appelle alphabet l'ensemble des symboles (caractères) composant la donnée de départ à compresser. Dans les parties A et B, nous utiliserons l'alphabet composé seulement des 8 lettres A, B, C, D, E, F, G et H.

Partie A (sur papier)

1) On cherche à coder chaque lettre de cet alphabet par une séquence de chiffres binaires.

1.a) Combien de bits sont nécessaires pour coder chacune des 8 lettres de l'alphabet ?

1.b) Quelle est la longueur en octets d'un message de 1000 caractères construit sur cet alphabet ?

2) Proposer un code de taille fixe pour chaque caractère de l'alphabet de 8 lettres.

3) On considère maintenant le codage suivant, la longueur du code de chaque caractère étant variable.

Lettre	A	B	C	D	E	F	G	H
Code	`10`	`001`	`000`	`1100`	`01`	`1101`	`1110`	`1111`

Ce type de code est dit préfixe, ce qui signifie qu'aucun code n'est le préfixe d'un autre (le code de A est 10 et aucun autre code ne commence par 10, le code de B est 001 et aucun autre code ne commence par 001). Cette propriété permet de séparer les caractères de manière non ambigüe.

3.a) En utilisant la table précédente, donner le code du message : CACHE.

3.b) Quel est le message correspondant au code 001101100111001.

4) Dans un texte, chacun des 8 caractères a un nombre d'apparitions différent. Cela est résumé dans le tableau suivant, construit à partir d'un texte de 1 000 caractères.

Lettre	A	B	C	D	E	F	G	H
Nombre	240	140	160	51	280	49	45	35

4.a) En utilisant le code de taille fixe proposé à la question 2), quelle est la longueur en bits du message contenant les 1000 caractères énumérés dans le tableau précédent ?

4.b) En utilisant le code de la question 3), quelle est la longueur du même message en bits ?

Partie B (sur papier)

1) L'objectif du codage de Huffman est de trouver le codage proposé dans la partie A.3. qui minimise la taille en nombre de bits du message codé, en se basant sur le nombre d'apparition de chaque caractère (un caractère qui apparait souvent aura un code plutôt court).

Pour déterminer le code optimal, on considère 8 arbres, chacun réduit à une racine, contenant le symbole et son nombre d'apparitions.

Puis on fusionne les deux arbres contenant les plus petits nombres d'apparitions (valeur inscrite sur la racine), et on affecte à ce nouvel arbre la somme des nombres d'apparitions de ses deux sous-arbres. Lors de la fusion des deux arbres, le choix de mettre l'un ou l'autre à gauche n'a pas d'importance. Nous choisissons ici de mettre le plus fréquent à gauche (s'il y a un cas d'égalité, nous faisons un choix arbitraire).

Figure 2 - Première étape : fusion des deux premiers arbres

Figure 3 - Deuxième étape : fusion des deux arbres suivants

On recommence jusqu'à ce qu'il n'y ait plus qu'un seul arbre.

Déterminer le nombre d'étapes (nombre de fusions d'arbres) nécessaires pour que cet algorithme se termine dans le cas étudié (figure 1).

2) En suivant l'algorithme précédent, terminer la construction de l'arbre de Huffman.

3) Le code à affecter à chaque lettre est déterminé par sa position dans l'arbre.

Précisément, le code d'un symbole de l'alphabet décrit le chemin de la racine à la feuille qui le contient : un 0 indique qu'on descend par le fils gauche et un 1 indique qu'on descend par le fils droit.

Dans le cas de l'arbre ci-dessous, le code de X est 00 (deux fois à gauche), le code de Y est 01, et celui de Z est 1.

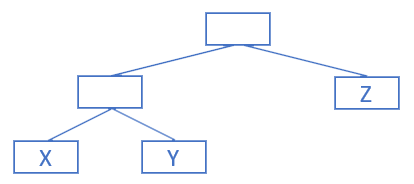
Sur chaque arête de l'arbre construit à la question 2), inscrire 0 ou 1 selon que l'arête joint un fils gauche ou un fils droit. Quel est le code de F ?

Partie C (sur ordinateur)

On souhaite écrire un programme qui, à partir d’un texte (dans une chaine de caractères), donne un dictionnaire contenant les lettres du texte comme clé et les codes binaires de Huffman correspondants comme valeurs.

Le programme se découpe en plusieurs parties :

- compter les occurrences des lettres ;
- construire l’arbre de Huffman ;
- parcourir l’arbre de Huffman pour donner les codes des lettres.

1) Création du dictionnaire des occurrences des lettres d’un texte

Compléter la fonction suivante.

def compte_occurrences(texte) :
    """
    Renvoie un dictionnaire contenant les occurrences des lettres d’un texte.
    Param texte : (str) texte à étudier
    Return : (dict)
    Exemple :
    >>> compte_occurrences("Bonjour !")
    {'B': 1, 'o': 2, 'n': 1, 'j': 1, 'u': 1, 'r': 1, ' ': 1, '!': 1}
    """

2) Construction de l’arbre de Huffman

On utilisera la classe suivante pour les arbres de Huffman.

class ArbreHuffman:
    def __init__(self, lettre, nbocc, g=None, d=None):
        self.lettre = lettre # attribut de type str
        self.nbocc = nbocc # attribut de type int
        self.gauche = g # g est un Arbre de Huffman ou None par défaut
        self.droite = d # d est un Arbre de Huffman ou None par défaut

    def est_feuille(self) -> bool:
        return self.gauche is None and self.droite is None

    def get_nbocc(self) -> int:
        return self.nbocc

    def __lt__(self, ah):
        # Cette méthode permet de considérer qu'un arbre est strictement inférieur à un autre arbre
        # si l'attribut nbocc du premier arbre est inférieur à l'attribut nbocc du deuxième.
        return self.nbocc < ah.nbocc

Remarque : la méthode __lt__(self, ah) permet de comparer deux arbres (lt pour lower than), ici en utilisant l’attribut nbocc. L’écriture __lt__ est spécifique à python et c’est cette fonction que python utilisera avec l’opérateur < entre deux instances de la classe ArbreHuffman ou avec la méthode sort() appliquée à une liste contenant des instances de la classe ArbreHuffman.

2.a) Écrire la fonction construit_liste_arbre_Huffman qui prend un dictionnaire d’occurrences en paramètre et renvoie une liste d’arbres de Huffman réduits à une feuille.

2.b) Écrire la fonction construit_arbre_Huffmman(list_ah) qui prend une liste d’arbres de Huffman réduits à une feuille en paramètre et les fusionne progressivement de façon à renvoyer un arbre de Huffman unique. On pourra utiliser la fonction sort() qui permet de trier une liste.

3) Parcours de l’arbre de Huffman

Les deux fonctions suivantes permettent de construire un dictionnaire dont les clés sont les lettres de l’arbre de Huffman et les valeurs des chaines correspondant aux nombres binaires.

def parcours(arbre, chemin_en_cours, dico):
    if arbre is None :
        return
    if arbre.est_feuille():
        dico[arbre.lettre] = chemin_en_cours
    else:
        parcours(arbre.gauche, chemin_en_cours + [0], dico)
        parcours(arbre.droite, chemin_en_cours + [1], dico)

def parcours_arbre_Huffman(arbreH):
    dico = {}
    parcours(arbreH, [], dico)
    return dico

Quelle est la spécificité de la fonction parcours(arbre, chemin_en_cours, dico) ?

4) Bilan

Écrire une fonction codage_Huffman(t) qui prend un texte en paramètre et renvoie un dictionnaire contenant les lettres du texte comme clés et les codes de Huffman correspondants comme valeurs.