C5.2 : Parcours d'un arbre binaire

Les différentes façons de parcourir un arbre binaire

Présentation

Le parcours d'un arbre commence par la racine.

Nous traiterons ici uniquement les parcours de gauche à droite.

Parcours en profondeur d'abord

Dans un parcours en profondeur d'abord, l'un des deux sous-arbres est entièrement exploré avant que l'exploration de l'autre commence.

On distingue trois cas :

  • • Le parcours préfixe : la valeur du nœud est récupérée avant l'exploration du sous-arbre de gauche et du sous-arbre de droite.
  • • Le parcours infixe : le sous-arbre de gauche est exploré d'abord, puis la valeur du nœud est récupérée, puis le sous-arbre de droite est exploré.
  • • Le parcours suffixe : le sous-arbre de gauche et le sous-arbre de droite sont explorés puis la valeur du nœud est récupérée.

Parcours en largeur d'abord

Dans un parcours en largeur d'abord, l'arbre est parcouru étage par étage.

Exemples

Considérons l'arbre suivant :

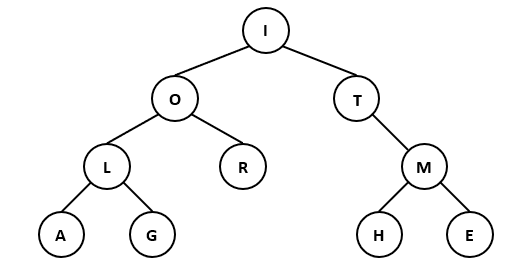
Q1 : Déterminer l'ordre des lettres pour chacun des parcours.

Codage des algorithmes de parcours

Choix de l'implémentation des arbres

Les arbres peuvent être implémentés en python avec des tuples imbriqués pour les arbres non vides (valeur, sous-arbre gauche, sous-arbre droit) et None pour l'arbre vide.

Q2 : Donner l'implémentation en python à base de tuples imbriqués (avec None pour l'arbre vide) de l'arbre du I.2 ?

Algorithmes de parcours en profondeur d'abord

Parcours infixe

Q3 : Proposer une fonction récursive qui permet de créer une chaine de caractères contenant les valeurs des nœuds d'un arbre avec un parcours infixe.

Afficher la correction 
def parcours_infixe(arbre):
    if arbre == None:
        return ""
    else:
        return parcours_infixe(arbre[1]) + str(arbre[0]) + parcours_infixe(arbre[2])

# ===== Programme principal ====
arbre = ("I",("O",("L",("A",None,None),("G",None,None)),("R",None,None)),("T",None,("M",("H",None,None),("E",None,None))))
print("Infixe : " + parcours_infixe(arbre))

Parcours préfixe

Q4 : Proposer une fonction récursive qui permet de créer une chaine de caractères contenant les valeurs des nœuds d'un arbre avec un parcours préfixe.

Afficher la correction 
def parcours_prefixe(arbre):
    if arbre == None:
        return ""
    else:
        return str(arbre[0]) + parcours_prefixe(arbre[1]) + parcours_prefixe(arbre[2])

# ===== Programme principal ====
arbre = ("I",("O",("L",("A",None,None),("G",None,None)),("R",None,None)),("T",None,("M",("H",None,None),("E",None,None))))
print("Préfixe : " + parcours_prefixe(arbre))

Parcours suffixe

Q5 : Proposer une fonction récursive qui permet de créer une chaine de caractères contenant les valeurs des nœuds d'un arbre avec un parcours suffixe.

Afficher la correction 
def parcours_suffixe(arbre):
    if arbre == None:
        return ""
    else:
        return parcours_suffixe(arbre[1]) + parcours_suffixe(arbre[2]) + str(arbre[0])

# ===== Programme principal ====
arbre = ("I",("O",("L",("A",None,None),("G",None,None)),("R",None,None)),("T",None,("M",("H",None,None),("E",None,None))))
print("Suffixe : " + parcours_suffixe(arbre))

Algorithme de parcours en largeur d'abord

L'un des façons de programmer le parcours en largeur, est d'utiliser une file d'arbre et une boucle simple.

On souhaite ici récupérer les valeurs dans une liste.

Le principe sera le suivant :

Créer une liste vide pour y stocker les valeurs de l'arbre.
Créer une file vide pour y stocker temporairement les arbres et sous-arbres lors du parcours.
Enfiler l'arbre dans la file.
Tant que la file n'est pas vide :
    Défiler et récupérer le premier arbre de la file.
    Si l'arbre n'est pas vide :
        Ajouter la valeur de l'arbre dans la liste.
        Enfiler le sous-arbre de gauche dans la file.
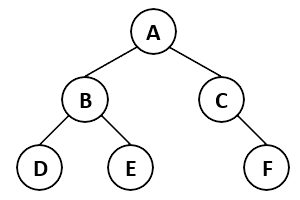
        Enfiler le sous-arbre de droite dans la file.

Q6 : Appliquer cet algorithme à l'arbre suivant, en détaillant étape après étape le contenu de la file et de la liste.

Q7 Coder cet algorithme en python. On pourra réutiliser le code de la classe File du chapitre 3.

Afficher la correction

Version où les files sont implémentées avec des objets list et les méthodes pop(0) et append(elt)

def parcours_largeur(arbre:tuple) -> list:
    """
    Fonction qui prend un arbre implémenté sous forme de tuples imbriqués en paramètre
    et renvoie la liste des étiquettes avec un parcours en largeur d'abord.
    """
    liste = []
    file_arbres = [arbre]
    while len(file) !=0:
        arbre = file_arbres.pop(0)
        if arbre is not None:
            liste.append(arbre[0])
            file_arbres.append(arbre[1])
            file_arbres.append(arbre[2])
    return liste

Version où les files sont implémentées avec la classe File vue dans le chapitre C3

class File:
    def __init__(self):
        self.__valeurs = []

    def est_vide(self):
        return len(self.__valeurs) == 0

    def enfile(self, val):
        self.__valeurs.append(val)

    def defile(self):
        if not(self.est_vide()):
            return self.__valeurs.pop(0)
        else:
            return None

def parcours_largeur(arbre:tuple) -> list:
    """
    Fonction qui prend un arbre implémenté sous forme de tuples imbriqués en paramètre
    et renvoie la liste des étiquettes avec un parcours en largeur d'abord.
    """
    liste = []
    file_arbres = File()
    file_arbres.enfile(arbre)
    while not file_arbres.est_vide():
        arb = file_arbres.defile()
        if arb is not None:
            liste.append(arb[0])
            file_arbres.enfile(arb[1])
            file_arbres.enfile(arb[2])
    return liste