C16.4 : TD - Le chercheur d'or
Présentation
But du TD
On s'intéresse ici à un chercheur d'or qui va creuser sa mine.
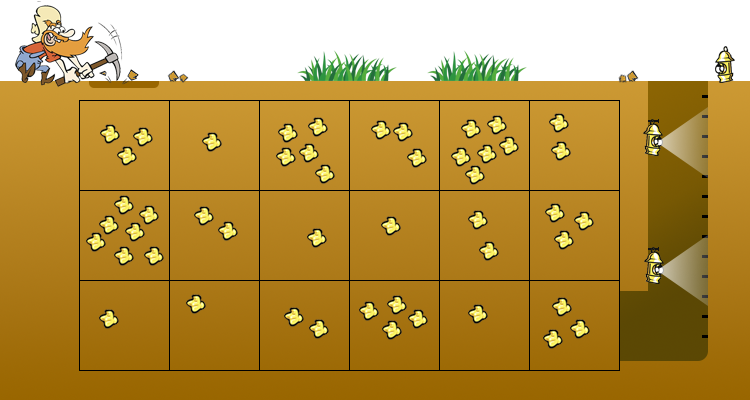
Le chercheur doit respecter deux contraintes :
- - Il doit commencer à creuser par la case en haut à gauche et terminer par la case en bas à droite.
- - Pour éviter les effondrements, il ne peut creuser que vers la droite ou vers le bas.
Le but de l'activité est d'écrire un programme pour aider le chercheur d'or à trouver le trajet qui lui permettra de récolter le plus de pépites.
Implémentation
La mine sera implémentée par une liste de listes où chaque valeur correspond au nombre de pépites d'une case.
Exemple :
mineA = [[3, 1, 5, 3, 6, 2],
[7, 2, 1, 1, 2, 3],
[1, 1, 2, 4, 1, 3]]
Programmation récursive simple
1) Proposer une fonction co_rec(mine:list, x:int, y:int)->int qui prend une mine et des coordonnées x,y en paramètres et permet de déterminer le plus grand nombre de pépites que le chercheur d'or peut ramasser.
2) Construire l'arbre des appels de la fonction.
3) Expliquer pourquoi on peut affirmer que cette fonction n'est pas optimale.
Programmation méthode glouton
1) Proposer une fonction co_glouton(mine:list)->int qui prend une mine en paramètre et renvoie, en se basant sur la méthode glouton, le plus grand nombre de pépites que le chercheur d'or peut ramasser.
2) Quel est le coût de cet algorithme en fonction de la largeur et de la hauteur de la mine ?
Programmation dynamique
Méthode ascendante
Ici, on utilise une liste de liste de la même taille que la mine, et dont les valeurs sont initialement à \(0\).
En commençant par la case \((0,0)\), on remplit la liste de liste en déterminant progressivement le nombre maximal de pépites que l'on peut ramasser pour chaque case.
1) Écrire la fonction co_dyn_asc(mine) qui renvoie le nombre maximal de pépites qu'il est possible de récolter.
2) Déterminer le coût de cet algorithme en fonction de la largeur et de la hauteur de la mine.
Méthode descendante (récursive)
Ici, on reprend la méthode récursive en y intégrant la mémorisation des résultats intermédiaires pour ne pas les calculer plusieurs fois. On pourra, pour cela, utiliser un dictionnaire dont les clés sont des tuples de coordonnées et les valeurs les nombres maximaux de pépites que l'on peut ramasser.
1) Écrire la fonction récursive co_dyn_desc(mine, x, y, dico) qui renvoie le nombre maximal de pépites qu'il est possible de récolter.
2) Déterminer le coût de cet algorithme en fonction de la largeur et de la hauteur de la mine, c'est-à-dire le nombre de récursion.
Prolongement : Programme complet
1) Écrire une fonction cree_mine(l, h) qui génère aléatoirement une liste de listes correspondant à une mine de largeur l et de hauteur h et dont les cases peuvent avoir entre 0 et 9 pépites.
2) Écrire une fonction affiche_mine(mine) qui affiche proprement une mine.
3) En reprenant et complétant de la fonction co_dyn_asc(mine), écrire une fonction trouve_max_et_chemin(mine) qui renvoie le nombre maximal de pépites et le chemin (liste de tuples) que le mineur doit suivre pour récolter le plus de pépites.
4) Écrire une fonction affiche_mine_chemin(mine, chemin) qui affiche proprement une mine et, en couleur, le chemin qui permet de récolter le plus d'or.
Le résultat attendu avec une mine de 6×4 est de la forme suivante :
