C5.1 : Les arbres binaires

Arborescence et arbres

Arborescence

De nombreuses situations de la vie courantes sont pensées sous forme d'arborescence :

• - la structure des chapitres, paragraphes, sous-paragraphe, etc d'un cours ;
• - d'une façon générale, toutes les classifications ;
• - l'organisation des dossiers et fichiers en mémoire d'un ordinateur...

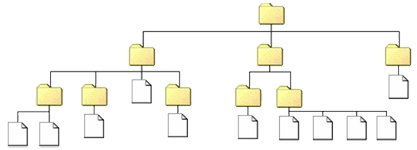
Une structure de données a été conçue pour cela en informatique : les arbres.

Quelques définitions des arbres

Applications

1) Proposer d'autres situations que celles du I.1 qui font appel à des arborescences.

2) Légender le schéma ci-dessous avec le vocabulaire des arbres.

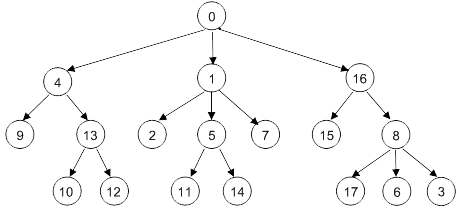
3) Comment sont appelées les feuilles dans une arborescence de dossiers et de fichiers ?

Les arbres binaires

Présentation

Propriétés d'un arbre binaire

Taille d'un arbre

Profondeur d'un nœud

Hauteur d'un arbre

Remarque

Il existe une autre façon de définir la profondeur d'un nœud et la hauteur d'un arbre.

Dans cette autre vision, la profondeur de la racine est égale à 0.

Exercices

Exercice 1

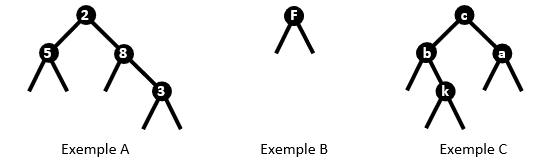
Donner la taille et la hauteur des trois arbres représentés au II.1

Exercice 2 : Arbres binaires d'une taille donnée

1) Représenter tous les arbres binaires de taille 3. Donner la hauteur de chacun de ces arbres.

2) Représenter tous les arbres binaires de taille 4. Donner la hauteur de chacun de ces arbres.

Exercice 3 : Arbres binaires d'une hauteur donnée

1) Représenter tous les arbres binaires de hauteur 2.

2) Représenter tous les arbres binaires de hauteur 3.

Encadrement de la hauteur d'un arbre

Considérons un arbre de taille \(t\) et de hauteur \(h\).

1) Quelle est la plus petite taille \(t_{min}\) d'un arbre binaire de hauteur \(h\) ? En déduire une inégalité entre \(t\) et \(h\).

2) Quelle est la plus grande taille \(t_{max}\) d'un arbre binaire de hauteur \(h\) ? En déduire une inégalité entre \(t\) et \(h\)

3) En déduire un encadrement de la taille \(t\) d'un arbre en fonction de sa hauteur \(h\).

Afficher la correction

Arbre de hauteur h de plus petite taille

Comme c'est la plus petite taille possible : \(t \ge h\)

Arbre de hauteur h de plus grande taille

Comme c'est la plus grande taille possible : \(t \le 2^h-1\)

Données :

• ⯀ \(1 + 2 + 3 + \text{...} + n = \dfrac{n(n+1)}{2}\)
• ⯀ \(1^2 + 2^2 + 3^2 + \text{...} + n^2 = \dfrac{n(n+1)(2n+1)}{6}\)
• ⯀ \(2^0 + 2^1 + 2^2 + \text{...} + 2^n = 2^{(n+1)} - 1\)

Implémentation en Python

Présentation

Il est possible d'implémenter les arbres binaires en utilisant des tuples.

Ainsi :

• - un nœud vide est une variable qui stocke la valeur None ;
• - un nœud non-vide sera un tuple contenant : la valeur, le sous-arbre de gauche, le sous-arbre de droite. Exemple : (valeur, arbre_gauche, arbre_droite)

L'écriture en python de l'exemple A du II.1 sera : (2,(5,None,None),(8,None,(3,None,None))).

Applications

Quelques exemples d'arbres binaires en python

1) Donner les écritures en pythons des arbres binaires des exemples B et C du II.1.

2) Proposer deux arbres de votre choix avec l'écriture en python et la représentation graphique.

Détermination de la taille et de la hauteur d'un arbre

def taille(arbre):
    if arbre == None:
        return 0
    else:
        return 1 + taille(arbre[1]) + taille(arbre[2])

def hauteur(arbre):
    if arbre == None:
        return 0
    else:
        return 1 + max(hauteur(arbre[1]), hauteur(arbre[2]))

# ==== Programme principal ====
a = (2,(5,None,None),(8,None,(3,None,None)))
print("Taille : " + str(taille(a)))
print("Hauteur : " + str(hauteur(a)))